Part 1 - The Martingale Strategy
On a recent trip to Las Vegas, a friend approached me with a simple gambling strategy that he believed to be foolproof. First, you bet the table minimum. If you win the first bet, you take the winnings. If you lose, however, you double your bet to recoup, repeating until you win a hand. At that point you go back to the table minimum.
For simplicityís sake, letís assume a table with a minimum bet of one dollar. If you have seven consecutive losses, but youíve doubled your bet each time, you will make it all back on the 8th and winning bet:
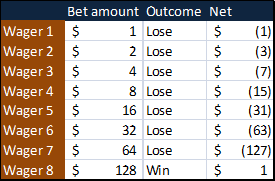
As long as you have enough money, he reasoned, you canít lose. And what are the odds of losing 7 wagers in a row, anyway?
If youíre ever been to Las Vegas, you realize that there is no foolproof gambling strategy. You donít build 100,000 square foot gambling floors by consistently paying out more than you take in. However, select individuals have found ways to consistently beat the house by counting cards in blackjack, studying roulette tables for imbalance, or even hacking slot machines. They say an economist is a person would walk by a $100 bill in the street without picking it up because the market says it canít exist. Could this strategy be a winner?
I quickly recognized the strategy as the Martingale system, developed hundreds of years ago in Europe. My initial thought was that the system was foolproof as long as:
- You begin with infinite money
- You have infinite time
- You had the psychological wherewithal to follow up a losing wager of $40,000 with one of $80,000, after you had just lost 12 hands in a row. Just as there are no atheists in foxholes, there are no Martingale players after 12 losses in a row.
To test it out, I decided to build a simulation in Excel. Simulation is a technique where the computer pretends to play out a situation hundreds or thousands of times to determine an expected outcome. I chose it over a mathematical proof based on probability because a) it is easier to test the effect of real-world limitations on a simulation and b) he wouldnít have understood it anyway.
This file shows what a single simulation would look like. It is defaulted to a $5 table with a maximum bet of $500. The player begins with $5,000 and is trying to earn $5,500. The imagined player will keep betting until he hits his goal, loses all his money, or runs out of time. You can modify the assumptions of the simulation by altering the blue cells:

The outcome box will show what happens to the player after a maximum of 400 rounds. Here is an example in which the player successfully reached his goal of $5,500:

His highest bet was $320, which means he hit an unlucky streak of 6 in a row before winning his money back. You could calculate this out by multiplication (5*2*2*2*2*2*2), but the great thing about computers is that you donít have to.
Each row in the spreadsheet will show you what happened in a single round: how much money the player began the round with, how much he bet, and how much money he ended with. Pressing the F9 key will run a new simulation.
This example shows the core of the Martingale Strategy:
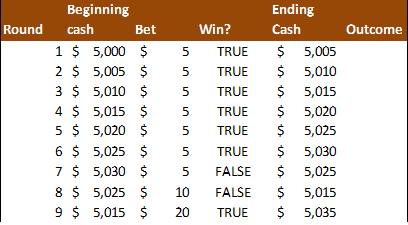
The playerís cash position moves up slowly by the amount of the minimum bet. He wins the first 6 rounds and is ahead $30. However, he loses the following 2 rounds, but makes it up when he wins a $20 bet on round 9. He has thus made up all the ground he lost, and is ready to face round 10 ahead of where he began. This brings up the first rule of the Martingale system: the wins are small and incremental.
In another simulation, we can see the impact of the maximum bet rule:
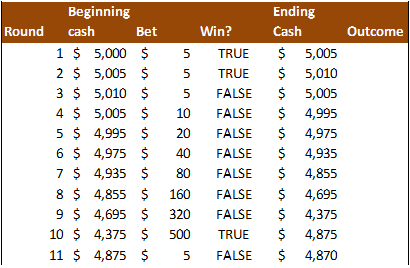
In round 10, the player would want to bet $640, or 2x his previous bet. However, he was stopped by the table rules and had to bet $500. When he won the hand, he ended at $4,875, which puts him in the hole for the series of bets. Had he been allowed to bet $640, he would have ended round 10 with $5,015, which is $5 above where he started the series in round 3.
This shows one way in which the casinos combat the Martingale system. It relies upon the ability to continue increasing bets in the face of losses. Consider this scenario, for instance:
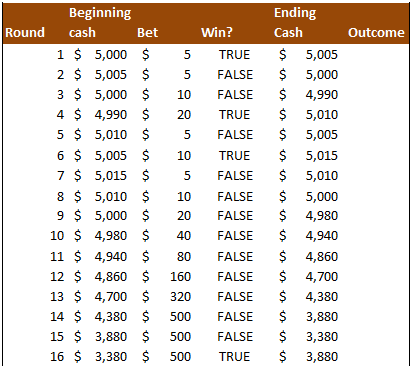
Here the player lost two successive $500 bets in rounds 14 and 15. Because he was not able to bet higher to cover the loss, he ended round 16 over $1,000 poorer than he entered round 7. In this particular scenario, he spent the 384 rounds trying to make up ground, ending at $4,165.
This leads us to the second lesson about the Martingale system: if you are going to use it, make sure that the table maximum will allow you to continue doubling your bet several times. There is only a 2% chance that you would lose 6 consecutive spins at roulette. That sounds low unless you are considering playing several hundred rounds.
Pressing F9 several times leads us to this simulation in which the player goes bust:
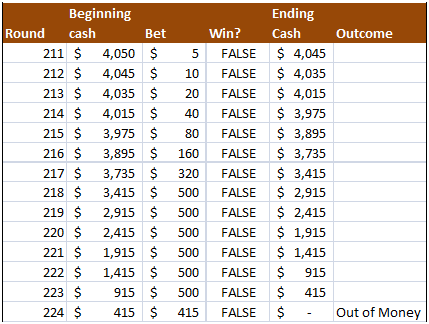
14 straight losses wipe out the playerís cash. There is only a .01% chance that a player would hit a streak that bad (one in 10,000) on any given 14 consecutive rounds. This is low odds, certainly, but I only had to hit F9 about 20 times to get it to happen. This brings us to the third lesson about the Martingale system: Make sure you begin with enough money to cover a string of bad luck. Low probabilities can appear if you play many rounds.
Interestingly, a string that bad would actually have been made worse by a lack of a table maximum. In an uncapped table, that playerís loss on round 224 would have been over $40,000.
In many simulations, the player is still playing after 400 rounds. Here is an example where, after 400 rounds, the player is up $115:

Assuming each round takes two minutes, this would have taken a little more than 13 hours. That translates to an hourly wage of $8.63, or about $1.50 above minimum wage. This brings us to the next lesson of the Martingale system: You had better be prepared to put in a lot of time to make progress.
This wraps up part one. Click here to continue on to part 2, To Simulate a Martingale.
