Part 3 - What the Martingale Strategy Can Teach us about Debt
In part one and part two, we examined the Martingale betting strategy, a system in which the player doubles his bet upon each successive loss in order to always make back his returns. Here are the key findings:
- The wins are small and incremental
- It will take you a long time to win money, but you can lose it all quickly
- You need to begin with a lot of money to use the strategy, sometimes in excess of 4000 times the minimum bet
- Most of the time the strategy will work, but it will occasionally fail catastrophically
Although there are few real-world situations in which someone doubles down on losses, the Martingale system has much to teach us about the financial system. Take, for instance, the first histogram we looked at in part 2:
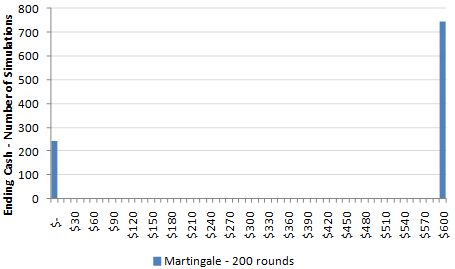
We simulated 1000 players using the strategy with a beginning bankroll of $500. Approximately 75% of the time, the players walked away with a profit of $100, which equates to a return of 20%. In the other 25% of the simulations, however, the players lost all of their money. This set of outcomes, or return profile, is similar to what you would see in any loan.
Consider, for instance, if you loan someone $500 at a 20% interest rate. They will either pay you back, giving you the $100 in profit, or they won’t, leaving you $500 in the hole. Whether you are making a loan to your brother-in-law, a business partner, or the Greek government, the expected return profile resembles that of a Martingale player.
Of course, most loans will not be total losses. A car loan is backed by the vehicle, a court may award damages on a lawsuit, and the Germans may chip in to repay investors. However, losses will often be severe. On a car loan, the lender will have to pay a repo man to get the vehicle back, pay a mechanic to fix any damage, and absorb the depreciation loss upon sale. The winner of a lawsuit will pay out legal fees and may get paid out less than he is owed, particularly if the other party has gone bankrupt.
More often, then, the return profile will look like our final simulation: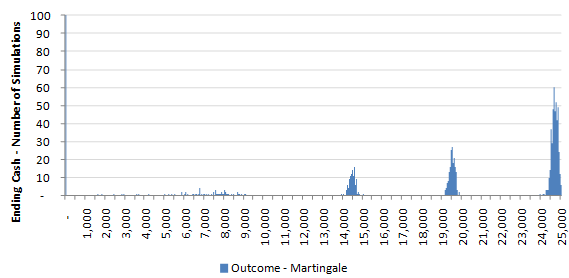
Here the player began with $20k. Most of the time, he would have a profit of $5k. Occasionally he would lose all of his money, and the rest of the time he would lose some but not all of his money. Reconsider this example as a car loan in which the bank loans someone $20k at a simple interest rate of 20%.
In the group of outcomes near $25k, the borrower pays back all of the payments on time leaving the bank with a profit. In the next group of outcomes to the left, the borrower makes payments for a few years and then defaults. The bank gets the car back without incident in good condition and is able to re-sell it at a decent price. Assume that the borrower makes $5k in payments to the bank before defaulting, and the bank is able to dispose of the vehicle for $15k. The whole thing is basically a wash for the bank, minus transaction costs.
In the next group of outcomes near $15k, the bank is taking a significant loss. Here, the borrower may have defaulted without making a single payment. Because it is no longer new, the vehicle has depreciated, and the bank can only get $15k for it. The bank is out $5k.
The lower probability outcomes near $8k could represent more unique situations. For instance, the vehicle is damaged when returned, or the bank spent a lot of money recovering it. In the final group of outcomes, the peak at $0, the bank is left with neither the car nor the money. Here, the borrower likely disappeared or totaled the vehicle.
If all loans have return profiles similar to the Martingale system, then the lessons we learned will also apply to any person or company making loans. In particular, a bank making 1000 car loans is very similar to the simulation we ran of 1000 gamblers.
The first lesson was the gains are small and incremental. For any debt instrument, the gains of the lender are capped from the start. In other words, the lender has a maximum profit that is agreed upon at the beginning of the transaction and his gains will accrue slowly over time. This is in contrast to a stock buy in which the party investing will share in the profits if the company is successful.
Consider, for instance, someone with $10k to invest in 1996. Assuming he has decided to invest in Apple, he has two choices: buy stock (equity) or bonds (debt). If he chose a ten year bond, he would have less than $20k in 2006. If he had bought the stock, however, he would have $86k. This is not to say that stocks will always outperform bonds, but to illustrate that the stock buyer has unlimited upside, while the bond buyer has a capped maximum. No matter how well a company performs, they will only pay the bond back at the interest rate that was set at the time.
The second lesson we learned was that it will take you a long time to make money, but you can lose it all quickly. This too is demonstrably true for any debt issuance. Our bond investor in Apple had to wait 10 years to earn $6,000. Apple nearly went out of business in 1997, which would have likely wiped him out. The bondholder may have walked away with some money, while the stock investor would have lost his entire investment. However, both would have suffered severe losses. My point is simply that the bond and stock investors both share similar risk of significant losses, while only the stock investor has substantial upside potential.
The third lesson was you need a lot of money to use the strategy. In our simulations, we saw that the gambler needed cash on hand to cover a string of bad luck. This is true for any entity making loans as well, particularly retail banks such as Bank of America. Retail banks make much of their money by making loans: car loans, mortgage loans, small business loans, credit card loans, etc. They are also funded by their own debt.
It is a bit counterintuitive, but when you deposit money in a bank you are actually making the bank a loan. After all, a loan is nothing but the act of giving money to a party with a promise of the money back at some point in the future. Savings accounts carry no maturity date, but the substance of the transaction is the same: you are giving the bank money with the expectation that it will repay you in the future.
When you make a deposit into a savings account, the bank does not keep all that money on hand. Instead, it lends it out to someone else, maintaining only a small amount on hand. This is called “fractional reserve banking,” an intentionally abstruse name designed to hide that if everyone came to cash out their savings accounts simultaneously, the bank would suffer a "run" and become insolvent. This happened hundreds of times in the 19th century, eventually leading to the establishment of FDIC insurance. This is also why banks are often architected in heavy stone: to give the appearance of stability.
Taken together, these three lessons show that retail banks are a particularly fragile type of entity. They are largely dependent upon making loans to make profits. However, these loans have a limited upside return, so the only way for them to make high profits is to issue a lot of debt. They are thus creatures of debt: great borrowers and issuers.
Lesson 1 and Lesson 3 are in opposition for banks. Lesson 1 tells us that the gains are small on any given loan, so the only way for banks to make a lot of money is to issue a lot of loans. Lesson 3, however, tells us that they need to have a lot of money on hand in case loans go bad and the borrowers do not repay. So the more money a bank keeps on hand to cover potential losses, the less money it has to loan out and make a profit. In fact, the Return on Assets is a commonly used measure of a bank’s value that encourages them to keep as little money on hand as possible.
Lesson 4 showed us that most of the time the strategy will work, but occasionally it will fail catastrophically. This is self-evident in the meltdown of 2008. Bank of America stock had quadrupled in the 15 years before the fall of 2007 and then lost 94% of its value in less than 2 years, including a drop from $32 per share to $3 per share in a single quarter, and would have been worthless if the federal government hadn’t bailed it out. This is due to its heavy position in issuing loans. Ken Lewis, the former CEO, is indistinguishable from a craps player who lost his life’s savings on a single roll of the dice.
Of course, the fact that debt is highly risky has been known for millennia. The bible warns us to "neither a borrower nor a lender be: and the Koran strictly forbids charging interest on a loan. In more recent history, debt failures caused the European debt crisis, the S&L crisis, the Latin American debt crisis, and countless others.
So, if banks know that issuing debt is highly risky, why do they keep doing it? The answer, like much in life, comes down to incentives. The people choosing whether or not to make particular loans are the management of the company, not the stockholders whose money is at risk. Read more in part 4 , What the Martingale Strategy Can Teach us about the Great Recession.
